what is rdbms
RDBMS stands for Relational Database Management System.
In HDBMS and NDBMS data is organized in the form of a tree structure which looks complex to manage and understand also. So to overcome this problem in 70’s dr. E F. codd from IBM came with a new concept on string the data in a table structure i.e. rows and columns of data.
E.F codd with all his ideas for the new model called as relational model has published an article with the title as “A relational model of Data for large shared data bank”.
Basing on this above article many companies came forward like IBM, Relational software INC(currently oracle) etc. has started the designed for the new database model i.e. RDBMS.
RDMS is mainly based on two mathematical principles relational algebra and calculus.
IN the year 70’s IBM has given the prototype for RDMNS known as “system R”.
In the year 1974 IBM has launched a language for communication with RDMNS known as SEQUEL.
The first relational data base was launched in the industry in the year 1978 with the name multi relational data store followed by Berkley ingress Quel and IBM Bs12
IN the year 1979 relational software INS has launched the most popular database in the market right now i.e. oracle.
Here relation can be defined as commonness between objects these relations are classified into 3 types
- One to One relation
- One to Many relation / Many to One relation
- Many to Many relation
One to One relationship:
In this relationship one object can have a relationship with another object.
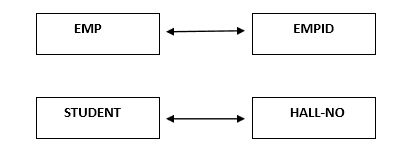
One to Many relationships:-
In this relationship one object can have a relationship with many objects.

Many to Many relationship:-
In this relationship many vendors (or) many objects can have the relationship with many other objects
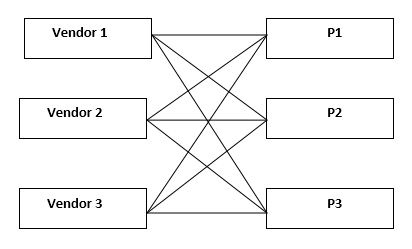
All the above relationships can be called as “Degree of Relationships”.
This model was developed on the basis of a mathematical concept can be called as “Relation Algebra” (i.e. sets & Relations).

